Олимпиадная задача по математике: эскалатор и скорость движения для 7-9 классов
Задача
По неподвижному эскалатору человек спускается быстрее, чем поднимается. Что быстрее: спуститься и подняться по поднимающемуся эскалатору или спуститься и подняться по спускающемуся эскалатору? (Предполагается, что все скорости, о которых идет речь, постоянны, причём скорости эскалатора при движении вверх и вниз одинаковы, а скорость человека относительно эскалатора всегда больше скорости эскалатора.)
Решение
Решение 1: Обозначим скорость эскалатора через v, скорости человека, поднимающегося и спускающегося по эскалатору, через v1 и v2 соответственно (тогда
v < v1 < v2). Длину эскалатора обозначим через l. Тогда время движения по поднимающемуся эскалатору равно
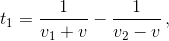а по спускающемуся эскалатору –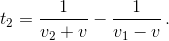 
Вычислим разность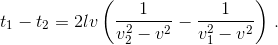 
По условию, знаменатели обеих дробей положительны, причём первый больше второго, поэтому всё выражение отрицательно. Вывод: t1 < t2.
Решение 2: Средняя скорость "поездки" в оба конца равна среднему гармоническому скорости подъема и скорости спуска. При фиксированном среднем арифметическом (оно в обоих случаях равно ½ (v1 + v2) среднее гармоническое больше тогда, когда числа находятся ближе к среднему арифметическому, то есть когда их разность меньше – в случае поднимающегося эскалатора.
Ответ
По поднимающемуся эскалатору.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь