Назад

Олимпиадная задача по математике: Докажите равенство для последовательности Курляндчика

Задача 198276 • Сложность: 2 • 7-9 класс
Задача

Последовательность определяется так: первые её члены – 1, 2, 3, 4, 5. Далее каждый следующий (начиная с 6-го) равен произведению всех предыдущих членов минус 1. Докажите, что сумма квадратов первых 70 членов последовательности равна их произведению.

Авторы:
Курляндчик Л. Д.
Разделы:
Многочлены Последовательности
Источники:
Турнир городов 17 турнир (1995/1996 год) осенний тур, основной вариант, 8-9 класс Олимпиады и турниры
Количество версий:
5
Решение

  Обозначим последовательность, о которой идёт речь в условии задачи, через {xn}. Введём новую последовательность {yn}: 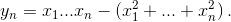    Вычислим  yn – yn+1  при  i ≥ 5:

 
  Так как  y5= 65,  то  y70=y5– 65 = 0.
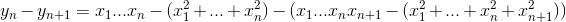
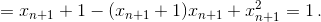
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет