Олимпиадная задача Васильева: разложение числа n на сомножители больше b, теория чисел
Задача
Пусть n и b – натуральные числа. Через V(n, b) обозначим число разложений n на сомножители, каждый из которых больше b (например:
36 = 6·6 = 4·9 = 3·3·4 = 3·12, так что V(36, 2) = 5). Докажите, что V(n, b) < n/b.
Решение
Индукция по n. База (n = 1) очевидна: V(1, b) = 0.
Шаг индукции. Предположим теперь, что это неравенство верно при всех m < n.
Для каждого делителя k > b числа n рассмотрим все разложения числа n, в которых минимальный сомножитель равен k. Количество таких разложений равно V(n/k, k – 1). Исключение составляет случай k = n – такое разложение одно, а V(n/n, n – 1) = 0. Следовательно,
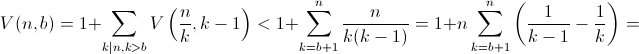
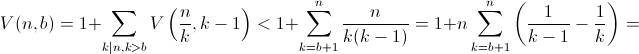
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет