Олимпиадная задача по математике: сравнение выражений с корнями и индукцией, 8-10 класс
Задача
Пусть m, n и k – натуральные числа, причём m > n. Какое из двух чисел больше: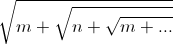 
или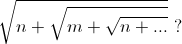 
(В каждом выражении k знаков квадратного корня, m и n чередуются.)
Решение
Обозначим эти числа xk и yk. Докажем по индукции, что 0 < xk – yk < m – n. База очевидна.
Шаг индукции.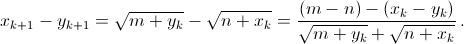 
По предположению индукции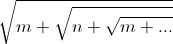 
Ответ
Первое число больше.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет