Олимпиадная задача Васильева Н. Б. по делимости и конструкциям для 8-9 классов

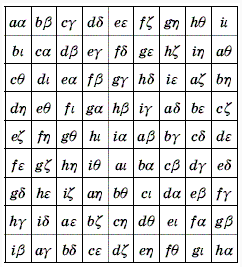
  Как и в задаче 198107, построим греко-латинский квадрат 9×9 (см. рис.). В нём:

  1) каждая клетка содержит по одной латинской и по одной греческой букве;

  2) в каждой строке и в каждом столбце все буквы различны;

  3) в каждых двух разных клетках пары букв различны.

  Поставим в соответствие выбранным буквам восемнадцать попарно различных попарно взаимно простых чисел и запишем в таблице вместо пары букв произведение соответствующих чисел. Произведение всех чисел каждого столбца и каждой строки будет равно произведению всех восемнадцати чисел. Если взять, например,  a = 1,  b = 2,  c = 3,  d = 5,  e = 7,  f = 11,  g = 13,  h = 17,  i = 19,  α = 23,  β = 29,  γ = 31,  δ = 37,  ε = 41,  ζ = 43,  η = 47,  θ = 53,  ι = 59,  то все числа в таблице будут различны, а максимальное число  iι = 19·59 = 1121.

Можно.