Олимпиадная задача по делимости: сумма квадратов и произведение чисел, 7–9 класс
Задача
Имеется n целых чисел (n > 1). Известно, что каждое из них отличается от произведения всех остальных на число, кратное n.
Докажите, что сумма квадратов этих чисел делится на n.
Решение
Пусть a1, ..., an – имеющиеся числа. а P – их произведение. По условию ai – P/ai кратно n. Тогда и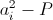 
кратно n. Сложив все такие выражения и прибавив Pn, получим сумму квадратов.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет