Назад

Олимпиадная задача по планиметрии и производной: площадь креста внутри круга

Задача 198037 • Сложность: 4 • 10-11 класс
Задача

Внутри круга радиуса R взята точка A. Через неё проведены две перпендикулярные прямые. Потом прямые повернули на угол φ относительно точки A. Хорды, высекаемые окружностью из этих прямых, замели при повороте фигуру, имеющую форму креста с центром в точке A. Найдите площадь креста.

Авторы:
Фольклор
Разделы:
Планиметрия Производная
Источники:
Турнир городов 11 турнир (1989/1990 год) осенний тур, основной вариант, 10-11 класс Олимпиады и турниры
Количество версий:
5
Решение

Зафиксируем перпендикулярные хорды BC и DE, проходящие через точку A, а хорды KL и MN будем поворачивать, увеличивая угол φ. Пусть S(φ) – интересующая нас площадь. При увеличении φ на малый угол δ площадь s(φ) криволинейного треугольника BAK увеличится на площадь криволинейного треугольника KAP (см. рисунок).

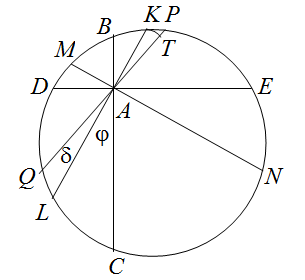
Последняя отличается от площади ½AK²δ сектораKATрадиусаAKс центром в точкеAи углом δ на площадь криволинейного треугольникаKPT, стороны которого не превышают 2Rδ. Следовательно,  SKPT< 4R²δ²  и производная     Значит, производная S′(φ) = ½ (AK² +AL² +AM² +AN²) = 2R²  (см. задачу156614). Так как  S(0) = 0,  то  S(φ) = 2R²φ.
Ответ

2φR².

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет