Олимпиадная задача по числовым последовательностям для 9-11 классов от Гальперина В.
Задача
Рассматривается последовательность слов, состоящих из букв "A" и "B". Первое слово в последовательности – "A", k-е слово получается из (k–1)-го с помощью следующей операции: каждое "A" заменяется на "AAB", каждое "B" – на "A". Легко видеть, что каждое слово является началом следующего, тем самым получается бесконечная последовательность букв: AABAABAAABAABAAAB...
а) На каком месте в этой последовательности встретится 1000-я буква "A"?
б) Докажите, что эта последовательность – непериодическая.
Решение
Обозначим n-е слово через Wn, а указанную операцию – через f: Wn+1 = f(Wn). Заметим, что f(UV) = f(U)f(V). Можно считать, что W0 = B. Поскольку W2 = W1W1W0, Wn+1 = WnWnWn–1. (*)
Пусть Wn содержит an букв A и bn букв B. Из (*) следует, что an+1 = 2an + an–1. (**)
По условию bn+1 = an. а) Вычисляем последовательно: a0 = 0, a1 = 1, a2 = 2, a3 = 5, a4 = 12, a5 = 29, a6 = 70, a7 = 169, a8 = 408, a9 = 985. Следовательно, 1000-я буква встретится уже в слове W10 = W9W9W8 = W9W5... = W9W4W4... = W9W4W3W3... = W9W4W2W2...
Слово W9 содержит 985 + 408 = 1393 буквы, слово W4 – 12 + 5 = 17 букв, W2W2 = AAВAAВ (помечена 1000-я буква A). Таким образом, 1000-я буква A находится на 1414-м месте (1393 + 17 + 4 = 1414). б) Предположим, что существует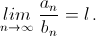 
Тогда и 
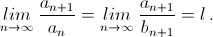Переходя к пределу в полученном из (**) равенстве 
видим, что l является корнем уравнения l = 2 + 1/l, то есть иррационально.
Предположим, что наша последовательность периодична, предпериод содержит c букв, период содержит a букв A, b букв B и укладывается kn раз в слове Wn. Тогда kna ≤ an < c + (kn + 1)a, knb ≤ bn < c + (kn + 1)b, значит,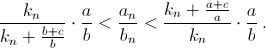 
Отсюда следует, что an/bn стремится к рациональному числу a/b. Противоречие.
Ответ
а) На 1414-м месте.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь