Олимпиадная задача по стереометрии и теории чисел для 8-11 классов: "Куб из кирпичей"

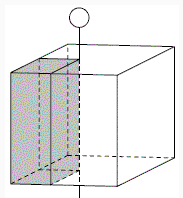
Каждую грань 20×20 куба можно проткнуть в  19·19 = 361  точке, а поскольку у куба три пары параллельных граней, всего имеется  361·3 = 1083  "возможных протыканий". Допустим, что куб нельзя проткнуть насквозь, то есть каждое из 1083 возможных протыканий заблокировано гранью 2×2 некоторого кирпича. Докажем, что каждое протыкание заблокировано чётным числом кирпичей. Введём иглу до конца и рассмотрим параллелепипед, закрашенный на рисунке.

В нём чётное (даже кратное 20) число единичных кубиков. С другой стороны, его составляют кирпичи 2×2×1 и "обломки" кирпичей 2×1×1 и 1×1×1. Следовательно, число кирпичей, которые наша игла проткнула (равное числу обломков 1×1×1 в параллелепипеде), чётно. Значит, общее число кирпичей не меньше  2·1083 > 2000.  Противоречие.

Ответ задачи отсутствует