Задача
Внутри правильного n-угольника взята точка, проекции которой на все стороны попадают во внутренние точки сторон. Этими точками стороны разделяются на 2n отрезков. Занумеруем их подряд: 1, 2, 3, ..., 2n. Доказать, что сумма длин отрезков с чётными номерами равна сумме длин отрезков с нечётными номерами.
Решение
Пусть точка M лежит внутри правильного n-угольника A1A2...An (будем считать, что длина его стороны равна 1), а O – его центр.
Обозначим 
Длина проекции отрезка A1M на сторону A1A2 равна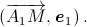 
Поэтому одна из сумм равна 
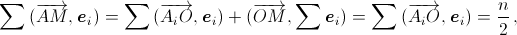то есть половине периметра многоугольника.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет