а) Пусть a и a₁ – первые клетки, окрашенные, соответственно, игроками К и С (см. рисунок). Вторым ходом К окрашивает клетку b, стоящую в одном столбце с a, так, что расстояние D между клетками b и a больше, чем между a₁ и a.

  После ответного хода С одна из клетокcиc₁того же столбца, находящихся сответственно отbиaна том же расстоянииD, (пустьc) останется неокрашенной. Её окрашивает К третьим ходом. Аналогично четвёртым ходом К окрашивает клеткуdилиd₁(которые находятся отcиaна расстоянии 2D). Допустим, он окрасилd, тогда рассмотрим столбцы, содержащие клеткиe, f, gиh. Один из них, например, содержащийe, свободен от синих клеток, потому что синих клеток всего четыре и одна из них –a₁– заведомо не стоит в этих столбцах. Окрасивe, игрок К получит выигрышную позицию (клеткиa, b, c, e): следующим ходом он "дополнит" до квадрата либо клеткиa, b, e, либо клеткиb, c, e.   б) Сначала К окрашивает 3⁸ произвольных клеток некоторой (первой) строки. Затем выбирает вторую строку, лежащую под всеми синими клетками, и окрашивает в ней клетки, лежащие под красными клетками первой строки. Очевидно, он успеет окрасить не менее трети таких клеток, то есть 3⁷. Далее аналогично выбирается третья строка и в ней окрашивается 3⁶ клеток, ..., выбирается седьмая строка и в ней окрашивается 3² клеток. Наконец К выбирает диагональ l, лежащую под всеми синими клетками, и окрашивает в ней три клетки, лежащие под красными клетками седьмой строки (а значит, и всех остальных строк).

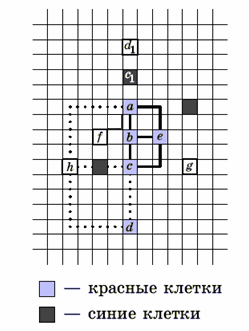
  Рассмотрим семь столбцов, в которых расположены клетки пересечения l с семью вышеупомянутыми строками. Так как на последнем этапе С закрасил синим шесть клеток, то в одном из этих столбцов новых синих клеток нет (а все старые лежат над l). К закрашивает клетку a пересечения этого столбца с l (и с некоторой – i-й – строкой). В результате образовалось три квадрата с общей "вершиной" а и еще двумя красными "вершинами" – на l и в i-й строке. Следующим ходом К "замкнёт" один из этих квадратов: С сможет "обезопасить" только два из них.

Ответ задачи отсутствует