Задача
а) Доказать, что для любых положительных чисел x1, x2, ..., xk (k > 3) выполняется неравенство:
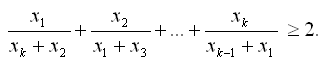
Решение
а) Применим метод математической индукции. Проверим неравенство для k = 4:
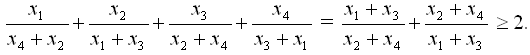
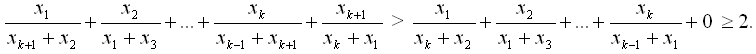
k – 2 остальных слагаемых меньше ε. Таким образом, левая часть меньше чем 2 + (k – 2)ε, то есть может быть сколь угодно близка к 2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет