Задача
Дан выпуклый четырёхугольник ABCD. Каждая его сторона разбита на k равных частей. Точки деления, принадлежащие стороне AB, соединены прямыми с точками деления, принадлежащими стороне CD, так что первая, считая от A, точка деления соединена с первой точкой деления, считая от D, вторая, считая от A, – со второй, считая от D, и т. д. (первая серия прямых), а точки деления, принадлежащие стороне BC, аналогичным образом соединены с точками деления, принадлежащими стороне DA (вторая серия прямых). Образовалось k² маленьких четырёхугольников. Из них выбрано k четырёхугольников таким образом, что каждые два выбранных четырёхугольника разделены хотя бы одной прямой первой серии и хотя бы одной прямой второй серии.
Доказать, что сумма площадей выбранных четырёхугольников равна 1/k SABCD.
Решение
Заметим, что каждый отрезок первой серии делится отрезками второй серии на k равных частей. Это немедленно следует из задачи 156471.
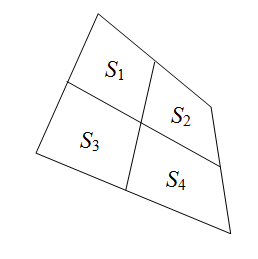
Теперь из задачи 155130 следует, что площади четырёхугольников одного ряда (заключенных между соседними прямыми первой серии) образуют арифметическую прогрессию (при k > 2). Причём разности этих прогрессий одинаковы. Действительно, для четырёх четырёхугольников с общей вершиной (см. рис.) согласно задаче 211654 S2 – S1 = S4 – S3.
Это же равенство решает задачу в случае k = 2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь