Задача
Решите неравенство: |x+ 2000| < |x- 2001|.
Решение
Решим неравенство, используя координатную прямую. Данное неравенство выполняется для всех точек c координатойx, которые находятся ближе к точке с координатой -2000, чем к точке с координатой 2001. Так как${\frac{-2000+2001}{2}}$= 0, 5, то искомыми являются все точки, расположенные левее точки с координатой 0, 5 (см. рис.). Возможны другие способы решения, в частности, раскрытие модулей (три случая); возведение обеих частей неравенства в квадрат.
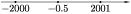
Ответ
(-$\infty$;0, 5).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет