Задача
Дана пирамидаАВСD(см. рис.). Известно, что $\triangle$ADB=$\triangle$DBC; $\triangle$ABD=$\triangle$BDC; $\triangle$BAD=$\triangle$ABC. Найдите площадь поверхности пирамиды (сумму площадей четырех треугольников), если площадь треугольникаАВСравна 10 см2.
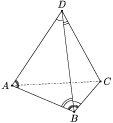
Решение
Используя признаки равенства треугольников, докажем, что все грани пирамиды - равные треугольники.
- $\triangle$ADB = $\triangle$CBD (II признак равенства треугольников), следовательно, AD = BC и AB = CD.
- $\triangle$ADB = $\triangle$ACB (I признак равенства треугольников).
- $\triangle$ABС = $\triangle$CDA (III признак равенства треугольников). Следовательно, все четыре треугольника имеют одинаковые площади.
Ответ
40 см2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет