Задача
Докажите, что если сумма косинусов углов четырёхугольника равна нулю, то он — параллелограмм, трапеция или вписанный четырёхугольник.
Решение
Пусть α, β, γ, δ — углы четырёхугольника. Тогда
0 = cos α + cos β + cos γ + cos δ = 2 cos$\displaystyle {\frac{\alpha+\beta}{2}}$cos$\displaystyle {\frac{\alpha-\beta}{2}}$ + 2 cos$\displaystyle {\frac{\gamma+\delta}{2}}$cos$\displaystyle {\frac{\gamma-\delta}{2}}$.
Так как α + β + γ + δ = 2π, то
cos${\frac{\alpha+\beta}{2}}$= − cos${\frac{\gamma+\delta}{2}}$. Следовательно,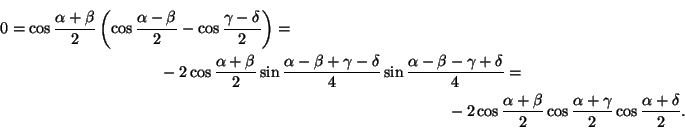
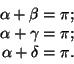
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет