Задача
В квадратной таблице из 9×9 клеток отмечены 9 клеток, лежащие на пересечении второй, пятой и восьмой строк со вторым, пятым и восьмым столбцами. Сколькими путями можно из левой нижней клетки попасть в правую верхнюю, двигаясь только по неотмеченным клеткам вверх или вправо?
Решение
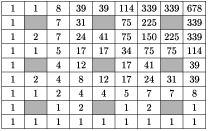
Пустьai,j– число путей из левой нижней клетки в клетку (i,j), не проходящих по отмеченным клеткам. Заметим, что если клетка (i,j) не отмечена, то ai,j=ai–1,j+ai,j–1 (а если отмечена, то ai,j= 0). Теперь несложно посчитать эти числа для каждой клетки доски (см. рисунок).
Ответ
678 путями.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет