Пустьl — данная прямая иB — данная точка. Сначала отметим на данной прямой две точкиAиM. После этого при помощи кронциркуля найдём на этой прямой такую точкуD, чтоAM=MD. Далее проведём прямуюABи отметим на ней за точкойBпроизвольную точкуE. После этого проведём прямыеBDиEMи обозначим черезOточку их пересечения. Теперь проведём прямыеAOиEDи обозначим точку их пересечения черезC. ПрямаяBC — искомая.

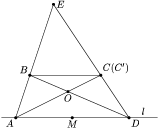
Докажем, что это действительно так, то есть чтоBC||AD. ПустьC' — такая точка на прямойED, чтоBC'||AD. В трапецииABC'Dточка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой. Следовательно, точка пересечения диагоналей трапецииABC'Dлежит на прямойEM, а значит, совпадает с точкойO. Таким образом, прямыеACиAC'совпадают, откуда следует и совпадение точекCиC'. Итак, прямаяBC — искомая.

Ответ задачи отсутствует