Задача
В некотором царстве, территория которого имеет форму квадрата со стороной 2 км, царь решает созвать всех жителей к 7 ч вечера к себе во дворец на бал. Для этого он в полдень посылает с поручением гонца, который может передать любое указание любому жителю, который в свою очередь может передать любое указание любому другому жителю и т.д. Каждый житель до поступления указания находится в известном месте (у себя дома) и может передвигаться со скоростью 3 км/ч в любом направлении (по прямой). Доказать, что царь может организовать оповещение так, чтобы все жители успели прийти к началу бала.
Решение
Организуем оповещение следующим образом. Разобьём царство на 4 квадрата со
стороной 1 км — квадраты 1-го ранга; каждый из этих квадратов разобьём на 4
квадрата со стороной 1/2 км— квадраты 2-го ранга, эти квадраты в свою
очередь на квадраты 3-го ранга (со стороной 1/4 км) и т. д., пока не дойдём
до столь большого рангаn, что в каждом квадрате этого ранга будет не более
одного жителя царства (жителей, попавших за общую границу нескольких
квадратов нужно произвольно распределить по этим квадратам). Оповещение будет
происходить поэтапно. Цель 1-го этапа — оповестить по одному жителю в
каждом из (населённых) квадратов 1-го ранга, после чего гонец и все посыльные
должны вернуться в исходные пункты. На 2-м этапе каждый из уже оповещённых
жителей, действуя как гонец на 1-м этапе, устраивает оповещение каждого из
квадратов 2-го ранга а своем квадрате 1-го ранга, на 3-м этапе оповещаются по
одному жителю в каждом квадрате 3-го ранга и т. д.. Послеn-го этапа будут
оповещены все жители.
 Оценим время, необходимое для 1-го этапа оповещения. Поскольку расстояние
между любыми двумя точками квадрата со стороной 2 км не превосходит
2$\sqrt{2}$км, при скорости 3 км/ч его можно пройти меньше чем за 1 ч.
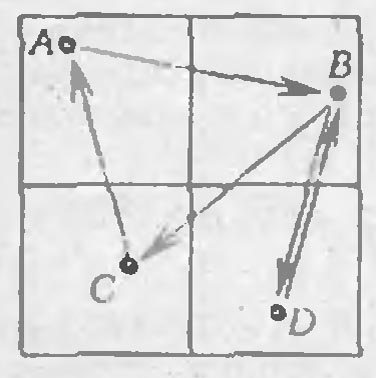
Поэтому по схеме, показанной на рисунке, 1-й этап можно осуществить не более
чем за 3 ч (гонецAоповещает жителейBиC, жительB- жителяD;
если в одном из квадратов 1-го ранга жителей не окажется, время оповещения
может только сократиться). Второй этап повторяет первый одновременно в
четырёх квадратах с вдвое меньшей стороной — он потребует не более 3/2 ч;
вообще,k-й этап осуществляется за$\displaystyle {\frac{3}{2^{k-1}}}$ч, а для оповещения всех жителей понадобится3 + 3/2 + ... +$\displaystyle {\frac{3}{2^{n-1}}}$< 6 ч.
Оценим время, необходимое для 1-го этапа оповещения. Поскольку расстояние
между любыми двумя точками квадрата со стороной 2 км не превосходит
2$\sqrt{2}$км, при скорости 3 км/ч его можно пройти меньше чем за 1 ч.
Поэтому по схеме, показанной на рисунке, 1-й этап можно осуществить не более
чем за 3 ч (гонецAоповещает жителейBиC, жительB- жителяD;
если в одном из квадратов 1-го ранга жителей не окажется, время оповещения
может только сократиться). Второй этап повторяет первый одновременно в
четырёх квадратах с вдвое меньшей стороной — он потребует не более 3/2 ч;
вообще,k-й этап осуществляется за$\displaystyle {\frac{3}{2^{k-1}}}$ч, а для оповещения всех жителей понадобится3 + 3/2 + ... +$\displaystyle {\frac{3}{2^{n-1}}}$< 6 ч.
Таким образом, к 6 часам вечера все жители получат приглашение на бал; ещё час им потребуется, чтобы прибыть во дворец.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь