Задача
Можно ли разбить множество целых чисел на три подмножества так, чтобы для любого целого значенияnчислаn,n- 50,n+ 1987 принадлежали трём разным подмножествам?
Решение
Ответ:нельзя. Доказательство проведём от противного. Предположим,
что указанное в условии разбиение существует. Будем писатьm
k, если целые числаmиkпринадлежат одному и тому же подмножеству разбиения, иm
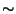k, если нет. Докажем, что
n n + 1937 и n
n − 150
для любого целогоn; отсюда будет следовать, что n + 1937 и n
n − 150
0 1937 2 . 1937 ... 50 . 1937 = 646 . 150 − 50 645 . 150 − 50 ... − 50,
т. е. 0 1937 2 . 1937 ... 50 . 1937 = 646 . 150 − 50 645 . 150 − 50 ... − 50,
− 50, а это противоречит условию задачи.
Назовем тройку чиселпредставительной, если она содержит по одному
числу от каждого подмножества разбиения. По условию тройки
n − 50, n, n + 1987; n − 100, n − 50, n + 1937 и n + 1937, n + 1987, n + 2 . 1987
— представительные при любом n (1937 = 1987 − 50).
В частности, из второй и третьей тройки видно, чтоn+ 1937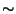n− 50 иn + 1937 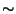n + 1987, а из первой — чтоn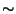n- 50 иn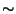n+ 1987. Отсюда следует наше первое утверждение:nn+ 1937. Теперь числоn + 1937 во второй тройке можно заменить наn, т. е. тройкаn− 100,n− 50,n — представительная. Подставляя в неёn− 50 вместоn, получим ещё одну представительную тройкуn− 150,n− 100,n− 50. Из сравнения этих двух троек вытекает второе утверждение:nn− 150.
Ответ
<style type="text/css"> div.p { margin-top: 7pt;}</style><style type="text/css"></style><title>Ответ</title>Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет