Площадь квадрата 2n×2nравна 4n², а площадь прямоугольника 1×(n+1) равнаn+1. Следовательно, число вырезанных прямоугольников не превосходит$\left[\vphantom{\frac{4n^2}{n+1}}\right.$${\frac{4n^2}{n+1}}$$\left.\vphantom{\frac{4n^2}{n+1}}\right]$, где [n] — целая часть числаn, то есть наибольшее целое число, не превосходящееn. Заметим, что

Следовательно, приn≥ 4 количество прямоугольников, которые может вырезать школьник, не превосходит 4(n− 1). Способ вырезать 4n − 4 прямоугольников показан на рисунке (дляn = 5).Осталось решить задачу приn≤ 3. Приn= 1 школьник хочет вырезать из квадрата размером 2×2 наибольшее количество прямоугольников размером 1×2. Ясно, что в этом случае ответ 2 (достаточно квадрат разрезать пополам любой из его средних линий). Приn= 2 школьник хочет вырезать из квадрата размером 4×4 наибольшее количество прямоугольников размером 1×3. Так как площадь квадрата равна шестнадцати, а площадь прямоугольника — трём, то можно вырезать не более пяти прямоугольников. Способ вырезать пять прямоугольников показан на рисунке.Приn= 3 школьник хочет вырезать из квадрата размером 6×6 наибольшее количество прямоугольников размером 1×4. Так как площадь квадрата равна 36, а площадь прямоугольника — четырём, то число вырезанных прямоугольников не превосходит девяти. Допустим, школьник смог вырезать девять прямоугольников. Это означает, что ему удалось разрезать квадрат 6×6 на прямоугольники 1×4. Ясно, что линии разреза параллельны сторонам квадрата, то есть каждая клетка полностью лежит в каком-нибудь прямоугольнике. Раскрасим клетки доски 6×6 как показано на рисунке. Так как число клеток цвета 1 не равно числу клеток цвета 2, а каждый прямоугольник 1×4 содержит по одной клетке каждого цвета, то квадрат 6×6 нельзя разрезать на прямоугольники 1×4. Следовательно, число прямоугольников не больше восьми. Способ вырезать восемь прямоугольников изображён на рисунке.

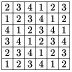
Ответ задачи отсутствует