Задача
Найдите минимум по всем α, β максимума функции
y(x) = |cos x + α cos 2x + β cos 3x|.
Решение
Ответ:$\min\limits_{\alpha,,\beta}^{}$$\max\limits_{x}^{}$y(x) =${\frac{\sqrt3}{2}}$и достигается при α = 0, β = −${\frac{1}{6}}$. При всех α и β справедливо неравенство
$\displaystyle \max\limits_{x}^{}$y(х) ≥ max(у($\displaystyle {\frac{\pi}{6}}$); y($\displaystyle {\frac{5\pi}{6}}$)) = max(|$\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$|; |− $\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$|) ≥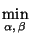 
(|$\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$| + |− $\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$|) ≥ $\displaystyle {\textstyle\frac{1}{2}}$|($\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$) − (− $\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$)| = $\displaystyle {\frac{\sqrt3}{2}}$,
поэтому$\min\limits_{\alpha,\,\beta}^{}$$\max\limits_{x}^{}$y(x) ≥${\frac{\sqrt3}{2}}$. Положим теперьf(x) = cos x−${\frac{1}{6}}$cos 3xи найдём точки экстремума этой функции из уравненияf'(х) = 0:f'(х) = − sin x + ${\frac{1}{2}}$ sin 3x = 0, −2 sin x+ (3 sin x− 4 sin3x) = 0, откуда либо sin x= 0,x=kπ, либо sin2x=${\frac{1}{4}}$,x= ±${\frac{\pi}{6}}$+kπ. Для функцииy(x) = |f(x)| имеем:y(kπ) =${\frac{5}{6}}$<${\frac{\sqrt3}{2}}$,y(±${\frac{\pi}{6}}$+kπ) =${\frac{\sqrt3}{2}}$.
Отсюда вытекает, что$\max\limits_{x}^{}$f(x) =${\frac{\sqrt3}{2}}$и поэтому$\min\limits_{\alpha,\,\beta}^{}$$\max\limits_{x}^{}$y(x) ≤${\frac{\sqrt3}{2}}$. (Решение из книги [Гальперин, Толпыго]).
(|$\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$| + |− $\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$|) ≥ $\displaystyle {\textstyle\frac{1}{2}}$|($\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$) − (− $\displaystyle {\frac{\sqrt3}{2}}$ + $\displaystyle {\frac{\alpha}{2}}$)| = $\displaystyle {\frac{\sqrt3}{2}}$,
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет