Представим произведение произвольной пары чисел  (a, b)  из данного набора в виде произведения квадрата натурального числа на произведение простых делителей в первых степенях (например, если  a = 2¹³·3⁴·19³,  b = 5⁶·7⁷·19,  то  ab = K²·2·7,  где  K = 2⁶·3²·5³·7³·19²).  Сопоставим паре  (a, b)  получившийся набор простых делителей. Всевозможных различных пар  (a, b)  в наборе из 48 чисел 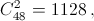    а количество наборов из 10 простых делителей (включая пустой набор)  2¹⁰ = 1024.  Так как  1128 > 1024,  то найдутся две различные пары  (a, b)  и  (c, d)  из набора, которым отвечает один и тот же набор  (p₁, p₂,..., p_k)  простых делителей  (0 ≤ k ≤ 10).  Следовательно, abcd – точный квадрат.

  Если при этом пары  (a, b)  и  (c, d)  не имеют общего элемента, то числа a, b, c, d – искомые. Если же общий элемент есть, например  b = d,  то тогда ac – точный квадрат. Выкинем на время числа a и c из рассмотрения. Тогда мы приходим к набору из 46 чисел, произведение которых имеет не более 10 различных простых делителей. Проведя те же рассуждения, что и выше, и учитывая, что 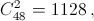    приходим к выводу о существовании двух различных пар чисел  (x, y)  и  (z, t)  из набора, для которых xyzt – точный квадрат. Если общего элемента у этих пар нет, то x, y, z, t – искомые четыре числа; если же общий элемент есть, например  x = t,   то yz – точный квадрат. В этом случае искомой четвёркой чисел является  (a, c, y, z).

Ответ задачи отсутствует