Задача
На бесконечной шахматной доске проведена замкнутая несамопересекающаяся ломаная, проходящая по сторонам клеток. Внутри ломаной оказалось k чёрных клеток. Какую наибольшую площадь может иметь фигура, ограниченная этой ломаной?
Решение
Будем постепенно перекрашивать нашу фигуру. На первом шаге перекрасим одну из чёрных клеток в синий цвет, а всех её белых соседей, принадлежащих фигуре, – в жёлтый. На следующем шаге перекрасим чёрную клетку, соседнюю с желтой, в синий цвет, а всех её белых соседей – в жёлтый. И так далее.
Поскольку фигура связная, а чёрных клеток ровно k, то ровно через k шагов вся фигура будет перекрашена. При этом на первом шаге перекрашиваются не более пяти клеток, а на каждом из остальных – не более четырёх (одна чёрная и три белых). Следовательно, всего в фигуре не более 4k + 1 клеток.
На рисунке приведён пример фигуры ровно из 4k + 1 клетки.
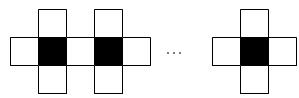
Ответ
4k + 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь