а)Ответ:можно. Докажем даже более общее утверждение: если правильно закрашены все клетки квадратаn×n, кроме некоторых клеток одной строки (или одного столбца), то квадрат можно правильно докрасить. Пусть, например, недокрашены некоторые клетки первой строки. Покрасим каждую такую клетку в тот цвет, который ещё не встречается в её столбце. Нужно доказать, что в первой строке при этом не может оказаться двух клеток одинакового, скажем, красного, цвета. Для этого рассмотрим прямоугольник (n− 1)×n, полученный из квадрата вычёркиванием первой строки. Поскольку раскраска была правильной, то в каждой изn− 1 строк прямоугольника красный цвет встречался один раз, — следовательно, всего красных клеток в немn− 1, а в каждом изnстолбцов прямоугольника красная клетка встречалась не более одного раза, — следовательно, красная клетка не встречалась только в одном из столбцов прямоугольника. Следовательно, лишь в одной клетке первой строки квадрата может появиться этот цвет. 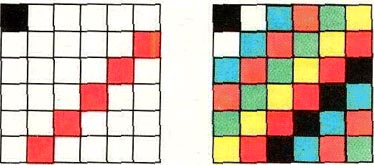б) и в)Ответ:вообще говоря, нельзя. Примеры приведены на рисунках (здесьn= 6; аналогичные примеры можно, конечно, привести и для любого n). Тот же ответ:нельзяверен, конечно, и для промежуточного междуnиn²− 2 числа закрашенных клеток (в качестве примера можно взять "промежуточный" между этими рисунками).

<style type="text/css"> div.p { margin-top: 7pt;}</style><style type="text/css"></style><title>Ответ</title>а) можно; б) и в) вообще говоря, нельзя.