Задача
Доказать, что среди чисел [2k·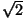 ] бесконечно много составных.
] бесконечно много составных.
Решение
Покажем, что среди таких чисел бесконечно много чётных.
Заметим, чтоk-я цифра двоичного разложения числа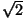 равна 1, если
число [2k$\sqrt{2}$] нечётно, и равна 0, если это число чётно. Если среди чисел [2k
равна 1, если
число [2k$\sqrt{2}$] нечётно, и равна 0, если это число чётно. Если среди чисел [2k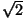 ] конечное число чётных, то начиная с какого-то места в двоичной записи числа
] конечное число чётных, то начиная с какого-то места в двоичной записи числа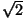 встречаются только единицы. Тогда оно
представимо в виде двоичной дроби, а значит, рационально. Получили
противоречие.
встречаются только единицы. Тогда оно
представимо в виде двоичной дроби, а значит, рационально. Получили
противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет