Задача
Задано такое натуральное число A, что для любого натурального N, делящегося на A, число 
тоже делится на A. ( – число, состоящее из тех же цифр, что и N, но записанных в обратном порядке; например, 
= 7691, 
= 54). Доказать, что A является делителем числа 99.
Решение
Заметим, что нули в конце числа N можно отбрасывать (если N = K·10t кратно A, причём число K не делится на 10, то по условию числа и 
= K кратны A).
Пусть N = a1a2...an–an кратно A и  an > 0. Вычитая из N·10n+2 число "в столбик", получим разность
M = a1a2...an–1(an – 1)99(9 – an)(9 – an–1)...(9 – a2)(10 – a1). Сложив теперь M с 
, получим число Y = 10
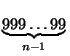, кратное A.
Если бы мы проделали те же действия, отправляясь от чисел N·10n+3 и , то получили бы число X = 10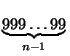, также кратное A. Но тогда
= 99  кратно A.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь