Задача
Дан многоугольник на плоскости, невыпуклый и несамопересекающийся. Д – множество точек, принадлежащих тем диагоналям многоугольника, которые не вылезают за его пределы (то есть лежат либо целиком внутри, либо частью внутри, частью на контуре). Концы этих диагоналей тоже включаются в Д. Докажите, что любые две точки из Д можно соединить ломаной, целиком принадлежащей Д.
Решение
Будем доказывать по индукции более сильное утверждение, состоящее из двух частей:
-
любые две точки множества Д можно соединить ломанной, целиком принадлежащей Д;
-
любая сторона n -угольника имеет общую точку с множеством Д.
При этом данный n -угольник может быть и выпуклым, n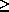 4.
4.
При n=4доказательство очевидно. Пусть теперь n произвольно. Так как n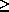 5,
то существует диагональ, целиком лежащая внутри многоугольника (известная задача
на принцип крайнего).
Разрежем многоугольник вдоль этой диагонали. К каждой из частей мы можем применить
предположение индукции (в случае, если одна из частей – треугольник,
достаточно применить предположение индукции ко второй части). Из утверждений 1) и 2)
для каждой из частей легко получаются утверждения
5,
то существует диагональ, целиком лежащая внутри многоугольника (известная задача
на принцип крайнего).
Разрежем многоугольник вдоль этой диагонали. К каждой из частей мы можем применить
предположение индукции (в случае, если одна из частей – треугольник,
достаточно применить предположение индукции ко второй части). Из утверждений 1) и 2)
для каждой из частей легко получаются утверждения
- и 2) для целого многоугольника.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь