Задача
Пирог имеет форму правильного n-угольника, вписанного в окружность радиуса 1. Из середин сторон проведены прямолинейные надрезы длины 1. Доказать, что при этом от пирога будет отрезан какой-нибудь кусок.
Решение
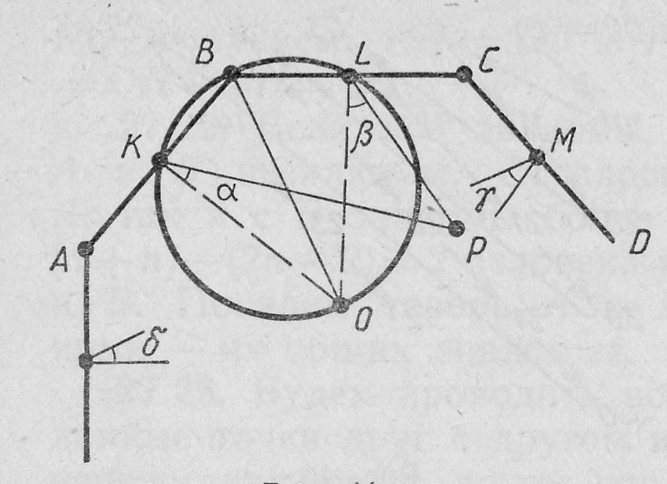
Пусть O – центр пирога. Легко видеть, что окружность, построенная на BO как на диаметре, проходит через середины K и L сторон сторон AB и BC (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет