Задача
Имеется бесконечное количество карточек, на каждой из которых написано какое-то натуральное число. Известно, что для любого натурального числа n существуют ровно n карточек, на которых написаны делители этого числа. Доказать, что каждое натуральное число встречается хотя бы на одной карточке.
Решение
Найдём, на скольких карточках написано число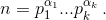 
Для этого найдём, на скольких карточках написаны делители числа n, меньшие n. Каждый такой делитель является делителем одного из чисел n/p1, ..., n/pk. Обозначим через Ai множество карточек, на которых написан один из делителей числа n/pi. Заметим, что Ai1 ∩ Ai2 ∩ ... ∩ Ail есть множество карточек, на которых написаны делители числа 
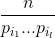. Следовательно, по условию
|Ai1 ∩ Ai2 ∩ ... ∩ Ail| = 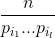, где |A| – количество элементов множества A. По формуле включения-исключения получаем, что число карточек, на которых написаны делители числа n, меньшие n, равно 
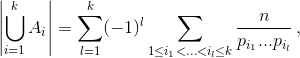откуда число карточек, на которых написано число n, равно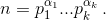 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь