Предположим, что существует замкнутая ломаная A₁...A_n с нечётным числом звеньев равной длины c, все вершины которой лежат в узлах целочисленной решётки. Пусть a_i и b_i – координаты проекций вектора    на горизонтальную и вертикальную оси. Тогда 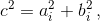   поэтому c² при делении на 4 даёт остаток 0, 1 или 2.

  Если c² делится на 4, то a_i и b_i чётны. Поэтому при гомотетии с центром A₁ и коэффициентом ½ наша ломаная перейдёт в ломаную с меньшей длиной звена, вершины которой по-прежнему лежат в узлах решётки. После нескольких таких операций придём к ломаной, у которой c² не делится на 4. Разберём оставшиеся варианты, предварительно заметив, что   a₁ + ... + a_m = b₁ + ... + b_m = 0.

  1)  c² ≡ 2 (mod 4).  Тогда числа a_i и b_i нечётны, поэтому число   a₁ + ... + a_m  нечётно и не может равняться нулю. Противоречие.

  2)   c² ≡ 1 (mod 4).  Тогда одно из чисел a_i и b_i нечётно, а другое чётно, поэтому число  a₁ + ... + a_m + b₁ + ... + b_m  нечётно и не может равняться нулю. Противоречие.

Ответ задачи отсутствует