Задача
Решить в целых числах уравнение 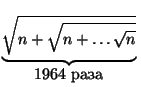 = m.
= m.
Решение
Решим в целых числах более общее уравнение Ay(x) = z, где Ay(x) =
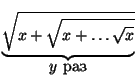 . Очевидно,
x + Ay–1(x) = z², или Ay–1(x) = z² – x.
. Очевидно,
x + Ay–1(x) = z², или Ay–1(x) = z² – x.
Таким образом, если число Ay(x) = z – целое, то и число Ay–1(x) = (z² – x) – целое; но тогда и число Ay–2(x) = (z² – x)² – x – тоже целое, и Ay–3 – целое, ..., и A1(x) = ![]() – целое. Следовательно, x = t² – целое (где t – целое).
– целое. Следовательно, x = t² – целое (где t – целое).
С другой стороны, для любого целого t (t², 1, t) – решение нашего уравнения.
Пусть y > 1. При этом числа A1(x) = ![]() = t и A2(x) =
= t и A2(x) = 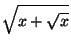 =
= ![]() =
= ![]() должны быть целыми. Но числа t и t + 1 – взаимно просты, откуда следует, что t и t + 1 – полные квадраты, то есть t = 0. Значит, x = 0 и Ay(x) = 0 при любом y.
должны быть целыми. Но числа t и t + 1 – взаимно просты, откуда следует, что t и t + 1 – полные квадраты, то есть t = 0. Значит, x = 0 и Ay(x) = 0 при любом y.
Ответ
(0, 0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь