Задача
Дана система из 25 различных отрезков с общим началом в данной точке A и с концами на прямой l, не проходящей через эту точку. Доказать, что не существует замкнутой 25-звенной ломаной, для каждого звена которой нашёлся бы отрезок системы, равный и параллельный этому звену.
Решение
Сумма векторов, отвечающих какому-нибудь прохождению звеньев замкнутой
ломаной, равна нулю. Каждый из них равен по модулю и направлению одному из
векторов ± ai, где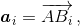 
а точки Bi лежат на прямой l. Таким образом, достаточно доказать, что
≠ 0 для любого набора εi = ±1. Рассмотрим проекцию любой такой комбинации на прямую m, перпендикулярную l. Пусть h – расстояние от точки A до прямой l, тогда проекция εiai равна εih. А значит, проекция вектора равна 
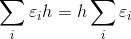≠ 0,
поскольку εi = ±1 и векторов нечётное число. Тем более ≠ 0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь