Задача
Лист клетчатой бумаги размером 5×n заполнен карточками размером 1×2 так, что каждая карточка занимает целиком две соседние клетки. На каждой карточке написаны числа 1 и –1. Известно, что произведения чисел по строкам и столбцам образовавшейся таблицы положительны. При каких n это возможно?
Решение
Так как произведение чисел в каждом столбце положительно, то минус единицы встречаются в каждом столбце, а значит, и во всей таблице чётное число раз. Следовательно, общее число карточек чётно, а общее число клеток в таблице (которое вдвое больше) делится на 4. Итак, 5n делится на 4; стало быть, n делится на 4.
Покажем теперь, что для любого n = 4k возможно требуемое размещение карточек. Для этого достаточно разместить карточки на листе размером 5×4 (см. рис.) и повторить это расположение k раз.
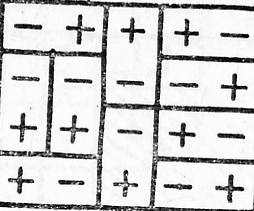
Ответ
При n, кратном 4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь