Проведём через точкуMпрямую, параллельнуюBN, и возьмём на ней такую точку Р, чтоBP||MN. Так какBPMN — параллелограмм, иMA, по условию, равноBN, то мы получаем:AM=MP, т. е. треугольникAMP — равнобедренный. Обозначим через$\alpha$угол между данными лучами (и, значит, между прямымиAMиMP). В таком случае

Мы видим, что$\angle$MAPне зависит от положения точкиMна лучеAO. Это значит, что точкаPвсегда лежит на некоторой вполне определённой прямой (составляющей угол$\displaystyle \beta$=$\displaystyle {\frac{180^{\circ}-\alpha}{2}}$с данным лучомAO). Заметим теперь, чтоPB=MN, а мы ищем такое положение точкиM, что отрезокMNминимален. Это, очевидно, произойдёт в том случае, когдаPB$\perp$AP, что и определяет выбор точки Р, а следовательно, и точкиM.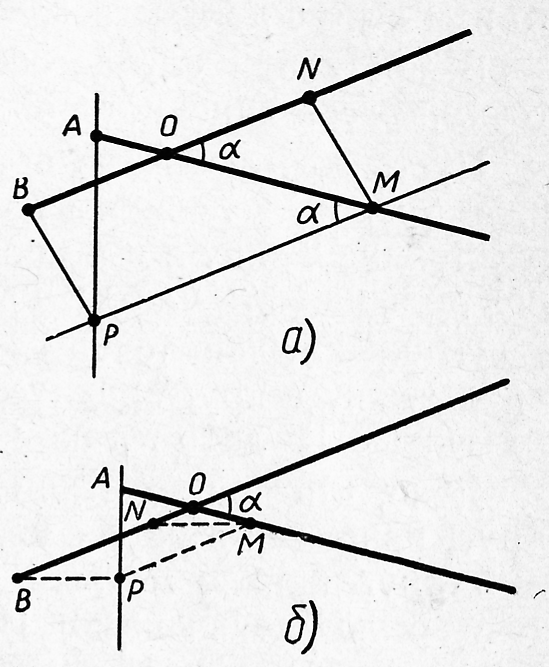

Ответ задачи отсутствует