Задача
Игральная доска имеет форму ромба с углом 60°. Каждая сторона ромба разделена на девять частей. Через точки деления проведены прямые, параллельные сторонам и малой диагонали ромба, разбивающие доску на треугольные клетки. Если на некоторой клетке поставлена фишка, проведём через эту клетку три прямые, параллельные сторонам и малой диагонали ромба. Клетки, которые они пересекут, будут считаться побитыми фишкой. Каким наименьшим числом фишек можно побить все клетки доски?
Решение
Заменим доску на эквивалентную квадратную доску 9×9, где во всех клетках проведены диагонали одного направления (рис. 1). Шести фишек достаточно, чтобы побить все клетки (см. рис. 1).
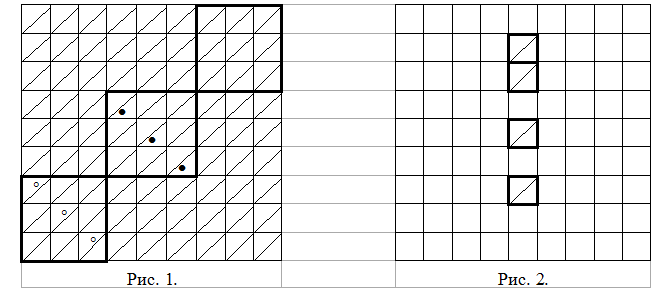
Пусть фишек только пять. Рассмотрим одну из вертикалей, на которойне стоитфишка. В ней есть как минимум четыреквадратика, не побитых погоризонтали. Им соответствует восемь клеток (рис. 2), никакие две из которых не могут быть одной фишкой побиты по диагонали. Таким образом, хотя бы три клетки не будут побиты ни одной фишкой.
Ответ
6 фишек.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь