Пусть  x_k = A_k+1B_k,  α — внешний угол правильного n-угольника, a — длина его стороны. Тогда  x₁ = (a + x₂) cos α,  x₂ = (a + x₃) cos α,  ...,

x_n = (a + x₁) cos α.  Тогда  x₁ = a₁ + b₁x₂ = a₂ + b₂x₃ = ... = a_n + b_nx₁,  где  b_n = (cos α)ⁿ ≠ 1.  Поэтому x₁ (а также и x_k для любого k) определено однозначно. Ясно также, что мы получим решение, если положим  x₁ = x₂ = ... = x_n = x,  где  x = (a + x) cos α,  то есть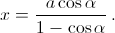  

Ответ задачи отсутствует