Задача
Дана замкнутая пространственная ломаная. Некоторая плоскость пересекает все её звенья:A1A2в точкеB1,A2A3— в точкеB2, ...,AnA1-- в точкеBn. Докажите, что
$\displaystyle {\frac{A_1B_1}{B_1A_2}}$$\displaystyle {\frac{A_2B_2}{B_2A_3}}$...$\displaystyle {\frac{A_nB_n}{B_nA_1}}$ = 1.
Решение
Рассмотрим проекцию на прямую, ортогональную плоскости сечения. Все точкиB1, ...,Bnпроецируются в одну и ту же точкуB. ПустьA1', ...,An' — проекции точекA1, ...,An. Тогда
$\displaystyle {\frac{A_1B_1}{B_1A_2}}$$\displaystyle {\frac{A_2B_2}{B_2A_3}}$...$\displaystyle {\frac{A_nB_n}{B_nA_1}}$ = 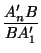
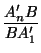 ...
...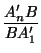 = 1.
= 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет