Назад

Сумма чисел при вычеркивании строк и столбцов в квадратной таблице

Задача 178034 • Сложность: 2 • 10-11 класс
Задача

Числа 1, 2, ..., k² расположены в квадратную таблицу

Произвольное число выписывается, после чего из таблицы вычеркивается строка и столбец, содержащие это число. То же самое проделывается с оставшейся таблицей из  (k– 1)²  чисел и т.д.kраз. Найти сумму выписанных чисел.
Разделы:
Текстовые задачи Алгебраические методы
Источники:
Московская математическая олимпиада 1955 год 9 класс, 1 тур Олимпиады и турниры
Количество версий:
5
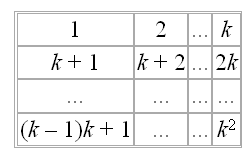
Решение

Запишем данную таблицу в виде

Каждое число таблицы представлено в виде  ka + b,  где  0 ≤a &le k– 1  и  1 ≤b ≤ k. Будем отдельно суммировать слагаемыеkaи слагаемыеb. Из каждой строки выписано в точности одно число, поэтому будут присутствовать слагаемыеkaдля каждого  a= 0, 1, ...,k– 1.  Из каждого столбца выписано в точности одно число, поэтому будут присутствовать слагаемыеbдля каждого  b= 1, 2, ...,k.  Таким образом, искомая сумма равна k(0 + 1 + 2 + ... + (k– 1)) + (1 + 2 + ... +k) = ½k(k(k– 1) + (k+ 1)) = ½k(k² + 1)).
Ответ

½ k(k² + 1)).

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет