Задача
Пусть x0 = 109,
xn = 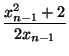 . Доказать, что 0 < x36 –
. Доказать, что 0 < x36 – ![]() < 10–9.
< 10–9.
Решение
xn – ![]() =
= 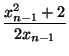 –
– ![]() =
= ![]() (xn–1 –
(xn–1 – ![]() )² > 0.
Кроме того, учитывая, что
)² > 0.
Кроме того, учитывая, что ![]() < 1, получаем xn –
< 1, получаем xn – ![]() <
< 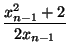 , (1)
, (1)
а, учитывая, что xn–1 > 1, получаем xn – ![]() <
< 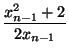 . (2)
. (2)
Из неравенства (1) следует, что xn – ![]() < x0·2–n. В частности, x30 –
< x0·2–n. В частности, x30 – ![]() < 109·2–30 = (1000/1024)³ < 1. Теперь, воспользовавшись неравенством (2), получим x31 –
< 109·2–30 = (1000/1024)³ < 1. Теперь, воспользовавшись неравенством (2), получим x31 – ![]() < ½,
x32 –
< ½,
x32 – ![]() < 2–3,
x33 –
< 2–3,
x33 – ![]() < 2–7,
x34 –
< 2–7,
x34 – ![]() < 2–15,
x35 –
< 2–15,
x35 – ![]() < 2–31,
x36 –
< 2–31,
x36 – ![]() < 2–63 < 2–30 < 10–9.
< 2–63 < 2–30 < 10–9.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет