Задача
В плоскости дан треугольник A1A2A3 и прямая l вне его, образующая с продолжением сторон треугольника A1A2, A2A3, A3A1 соответственно углы α3, α1, α2. Через точки A1, A2, A3 проводятся прямые, образующие с l соответственно углы π – α1, π – α2, π – α3. Доказать, что эти прямые пересекаются в одной точке. Все углы отсчитываются от прямой l в одном направлении.
Решение
Введём на плоскости систему координат, выбрав прямую l в качестве оси x. Пусть (a1, b1), (a2, b2), (a3, b3) – координаты вершин A1, A1, A3. Прямая A2A3 задаётся уравнением
= 
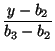. Прямая, проведённая через вершину A1, задаётся уравнением, в котором отношение коэффициентов при x и y то же самое по абсолютной величине, но имеет противоположный знак. Таким образом, эта прямая задаётся уравнением
+ 
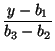= 0.
Напишем аналогично уравнения прямых, проведённых через вершины A2 и A3. Умножим левые части этих уравнений на (a3 – a2)(b3 – b2),
(a1 – a3)(b1 – b3), (a2 – a3)(b2 – b3) соответственно и сложим их. Легко проверить, что указанная сумма тождественно равна нулю. Из этого следует, что что точка пересечения двух прямых принадлежит третьей, то есть все три прямые пересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь