Предположим, что многочлен  3x²ⁿ + Axⁿ + 2  делится на многочлен  2x^2m + Ax^m + 3.  Тогда каждый корень многочлена  2x^2m + Ax^m + 3  является также корнем многочлена  3x²ⁿ + Axⁿ + 2.  Если x_i – корень многочлена  2x^2m + Ax^m + 3,  то 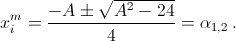    Можно считать, что  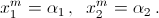   Пусть 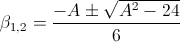    – корни квадратного трёхчлена 3x² + Ax + 2.

  Рассмотрим два случая.

  1)  A² – 24 > 0.  В этом случае   |α₁| ≠ |α₂|,  поэтому     С одной стороны,  

а с другой, 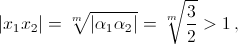    Противоречие.

  2)  A² – 24 < 0.  В этом случае 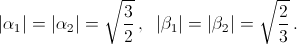    Поэтому, с одной стороны,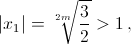  

а с другой, 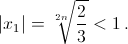    Снова противоречие.

Ответ задачи отсутствует