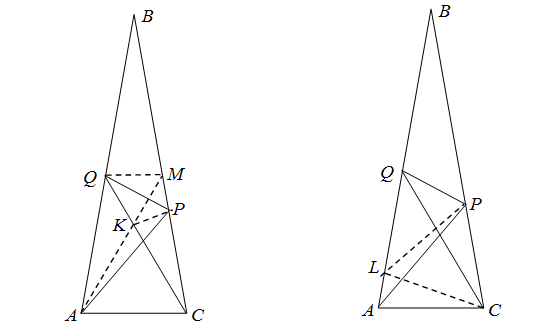
Решение 1:   Выберем на стороне BC точку M так, что  ∠CAM = 60°.  Пусть K – точка пересечения прямых CQ и AM (рис. слева). Легко видеть, что  ∠APC = 50°.  Поэтому треугольник ACP равнобедренный, а значит,  PC = AC = KC.  Угол при вершине C равнобедренного треугольника PCK равен 20°, поэтому  ∠KPC = 80°,   а  ∠MKP = 120° – 80° = 40°.  Но и  ∠KMP = 40°.  Значит, точка P равноудалена от точек M и K.

  Точка Q также равноудалена от M и K, следовательно, прямая QP – серединный перпендикуляр к отрезку MK, то есть является высотой (и биссектрисой) равностороннего треугольника KQM.

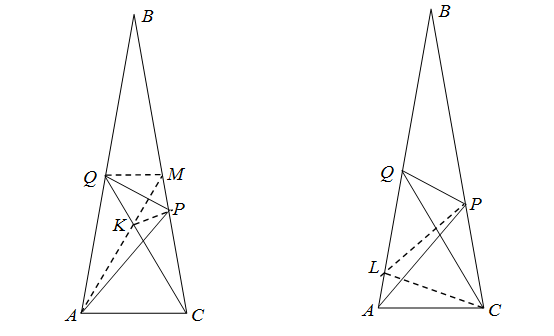
Решение 2:   Заметим, что  AC = РC  (см. решение 1). На стороне AB отметим точку L, для которой  ∠ACL = 20°  (см. рис. справа). Тогда  ∠CAL = ∠ALC = 80°,  значит, треугольник ACL – равнобедренный  (AC = CL).  В треугольнике СPL  ∠PCL = 60° и CP = CL,  следовательно, он равносторонний. Угол CQL – внешний для треугольника CQВ, поэтому  ∠CQL = 40° = ∠QCL.  Следовательно, треугольник CLQ также равнобедренный  (CL = QL).  Поскольку  QL = CL = PL,  треугольник PLQ равнобедренный, и  ∠LPQ = ∠PQL = ½ (180° – ∠PLQ) = 70°.  Поэтому,  ∠CQP = 70° – 40° = 30°.

Решение 3:   Докажем подобие треугольников ABP и QCP. Так как  ∠ABP = ∠QCP = 20°,  то достаточно проверить, что  AB : QC = BP : CP.  Пусть

АВ = BC = 1,  тогда  AC = 2 sin 10°,  а из равнобедренного треугольника CQВ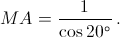   

  CP = AC  (см. решение 1), значит,  BP = СB – AP = (1 – 2 sin 10°).  Таким образом,

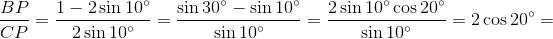
Решение 4:   Рассмотрим правильный восемнадцатиугольник А₀А₁...А₁₇, вписанный в окружность с центром B. Пусть  C = А₀  и  А = А₁,  тогда рассматриваемый треугольник АBC совпадёт с треугольником А₁BА₀. Так как  ∠А₀А₁А₁₃ = 50°,  то диагональ А₁А₁₃ пересекает BC в точке P. Так как диагонали А₁₇А₅ и А₁А₁₃ симметричны относительно диаметра А₀А₉, то А₅А₁₇ проходит через точку P. Так как  ∠А₁А₀А₇ = 60°,  то диагональ А₀А₇ пересекает АB в точке Q.

  Согласно задаче 157072 а), диагонали А₀А₇, А₅А₁₇ и А₁А₁₀ пересекаются в одной точке – точке Q. Тогда  ∠CQP = ∠А₀QА₁₇  измеряется полусуммой дуг А₀А₁₇ и А₅А₇, то есть равен 30°.

Ответ задачи отсутствует