Задача
При делении многочлена x1951 – 1 на x4 + x³ + 2x² + x + 1 получается частное и остаток. Найти в частном коэффициент при x14.
Решение
Равенства x4 + x³ + 2x² + x + 1 = (x² + 1)(x² + x + 1) и x12 – 1 = (x – 1)(x² + x + 1)(x³ + 1)(x² + 1)(x4 – x² + 1) показывают, что
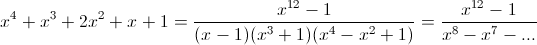
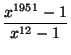 =x1939+x1927+x1915+ ... +x19+x7+
=x1939+x1927+x1915+ ... +x19+x7+ , поэтому искомый коэффициент равен коэффициенту приx14в произведении
, поэтому искомый коэффициент равен коэффициенту приx14в произведении 
Ответ
–1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет