Задача
Решить систему уравнений:
x + y = a,
x5 + y5 = b5.
Решение
Пусть a = 0. Если b ≠ 0, решений нет, если b = 0 – бесконечное множество решений вида (t, – t).
Пусть a ≠ 0. Положим xy = t. Тогда x5 + y5 = (x + y)5 – 5(x + y)³xy + 5(x + y)x²y² = a5 – 5a³t + 5at².
Решая квадратное уравнение 5at² – 5a³t + a5 – b5 = 0, находим 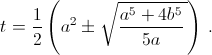 Дальнейшие вычисления имеют смысл при
Дальнейшие вычисления имеют смысл при
a(a5 + 4b5) ≥ 0. В результате получаем систему уравнений x + y = a, xy = t.
Таким образом, x, y – решения уравнения z² – az + t = 0, то есть равны
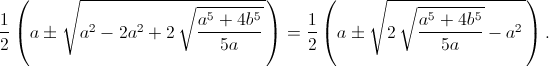
Ответ
При a = b = 0 – бесконечное множество решений вида (t, – t);
при 16b5 ≤ a5 < 0 и 0 < a5 ≤ 16b5 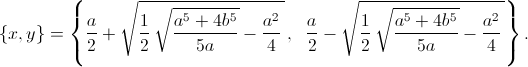
В остальных случаях решений нет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет