а) Первый способ. См. задачу 130371.

  Второй способ. Пусть 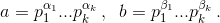    Тогда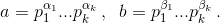  

  Поэтому доказательство можно провести для каждого простого множителя отдельно. Если  a = p^α,  b = p^β,  причём  α ≤ β, то  (a, b) = p^α,

[a, b] = p^β  и  [a, b](a, b) = p^αp^β = ab.   б) Достаточно рассмотреть случай, когда  a = p^α,  b = p^β, c = p^γ, причём  α ≤ β ≤ γ.  В этом случае

[a, b, c](a, b)(b, c)(c, a) = p^γp^αp^βp^α = p^αp^αp^βp^γ = (a, b, c)abc.

Ответ задачи отсутствует