Задача
Сколькими различными способами можно разложить натуральное число n на сумму трёх натуральных слагаемых? Два разложения, отличающиеся порядком слагаемых, считаются различными.
Решение
Первый способ. Пусть n = x + y + z. Число x может быть равно 1, 2, 3, ..., n – 2. При фиксированном x число y может принимать одно из
n – x – 1 значений. Всего получаем (n – 2) + (n – 3) + ... + 1 = ½ (n – 1)(n – 2) вариантов. Второй способ. Запишемnкак сумму единиц: n= 1 + 1 + ... + 1. Среди n– 1 знаков плюс мы должны выбрать два: те единицы, что стоят перед первым по порядку выбранным знаком плюс, в сумме дают числоx, а те, что стоят после второго знака плюс, – числоz. Всего получаем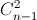 
вариантов.
Ответ
½ (n – 1)(n – 2) способами.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь