Задача
Решить систему уравнений:
x² + y² – 2z² = 2a²,
x + y + 2z = 4(a² + 1),
z² – xy = a².
Решение
(4(a² + 1) – 2z)² = (x + y)² = x² + y² + 2xy = 2z² + 2a² + 2(z² – a²) = 4z², откуда 16(a² + 1)² = 16(a² + 1)z, то есть z = a² + 1. Теперь второе и третье уравнения записываются так:
x + y = 2(a² + 1),
xy = a4 + a² + 1.
Решение этой системы сводится к решению квадратного уравнения t² – 2(a² + 1)t + a4 + a² + 1 = 0; решая его, находим 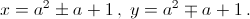
Ответ
(a² + a + 1, a² – a + 1, a² + 1), (a² – a + 1, a² + a + 1, a² + 1).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет