Задача
Два подмножества множества натуральных чисел называют конгруэнтными, если одно получается из другого сдвигом на целое число.(Например, множества чётных и нечётных чисел конгруэнтны.)Можно ли разбить множество натуральных чисел на бесконечное число
Решение
Покажем, как построить требуемое разбиение. Разбиение однозначно задается функцией f:N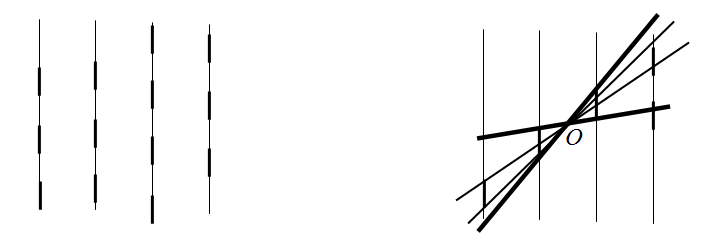 N на множестве N натуральных чисел, сопоставляющей натуральному числу номер множества,
которому оно принадлежит. Определим функцию f на отрезке[2k-1+1;2k]индуктивно
по следующим правилам:
N на множестве N натуральных чисел, сопоставляющей натуральному числу номер множества,
которому оно принадлежит. Определим функцию f на отрезке[2k-1+1;2k]индуктивно
по следующим правилам:
1) f(1)=1.
- Пусть f(x)уже определено для всех x
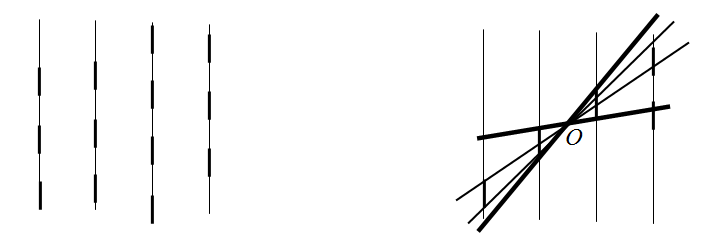 2k-1, а y
2k-1, а y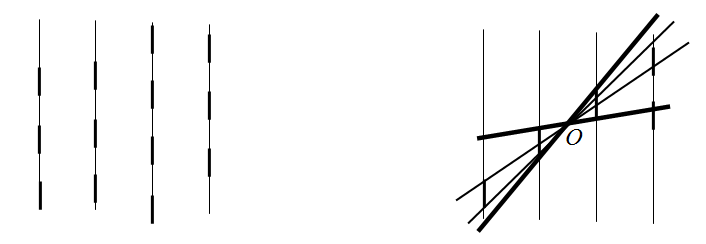 [2k-1+1;2k].
Тогда положим f(y)=f(y-2k-1)при k четном и f(y)=f(y-2k-1)+2s при k=2s+1нечетном.
[2k-1+1;2k].
Тогда положим f(y)=f(y-2k-1)при k четном и f(y)=f(y-2k-1)+2s при k=2s+1нечетном.
Легко проверить, что эта функция f задает требуемое разбиение.
Ответ
<style type="text/css"> div.p { margin-top: 7pt;}</style><style type="text/css"></style><title>Ответ</title>Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь