Задача
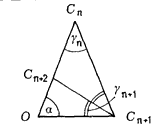
Дан треугольник C1C2O. В нём проводится биссектриса C2C3, затем в треугольнике C2C3O – биссектриса C3C4 и так далее.
Докажите, что последовательность величин углов γn = Cn+1CnO стремится к пределу, и найдите этот предел, если C1OC2 = α.
Решение
Из условия следует, что Cn+1Cn+2 – биссектриса угла треугольника Cn Cn+1O (см. рис.), поэтому 2γn+1 + γn + α = π. (1)
Ответ
π–α/3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет